1、八数码游戏简介
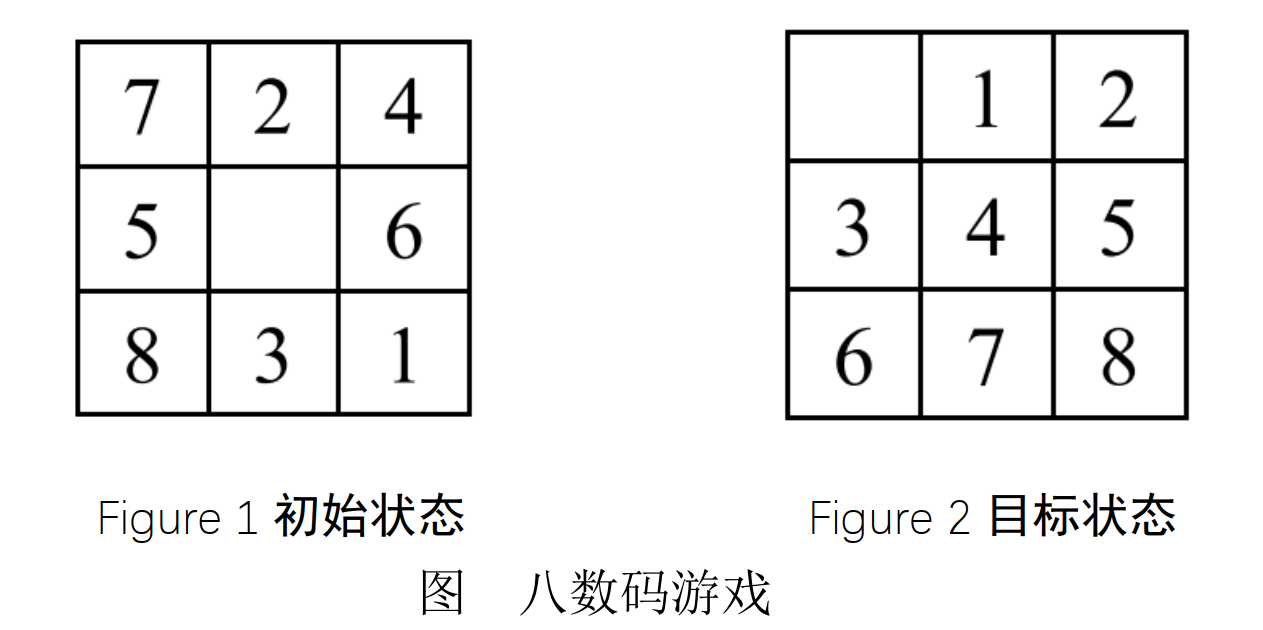
八数码问题(又称九宫排字问题)是人工智能中有名的难题之一。问题是在3×3方格盘上,放有八个数码:从1到8,剩余第九个为空也可以用0来表示,每一空格的周围的数码可移至空格。
问题给定初始状态和目标状态,要求通过一系列的数码移动,将初始状态转化为目标状态。
2.问题的形式化
2.1 状态
该问题,由9个空格组成,需要由初始状态移动成为目标状态,但是每次只能将空格旁的数字进行位置的互换,也就是说,该问题的每一个状态都是空格进行“向上”、“向下”、“向左”、“向右”,运动后的状态即:八个数字滑块每个占据一个方格,而空格(0)位于最后一个方格。
2.2 行动
1、当空格在正中间时,空格可以进行上下左右的移动。但是当空格在外围时,就要具体分析:
(1) 在正左边时,可以“向上”、“向下”、“向右”;
(2) 在正右边时,可以“向上”、“向下”、“向左”;
(3) 在正上边时,可以“向下”、“向左”、“向右”;
(4) 在正下边时,可以“向上”、“向左”、“向右”;
(5) 在左上角时,可以“向下”、“向右”;
(6) 在右上角时,可以“向下”、“向左”;
(7) 在右下角时,可以“向上”、“向左”;
(8) 在左下角时,可以“向上”、“向右”;
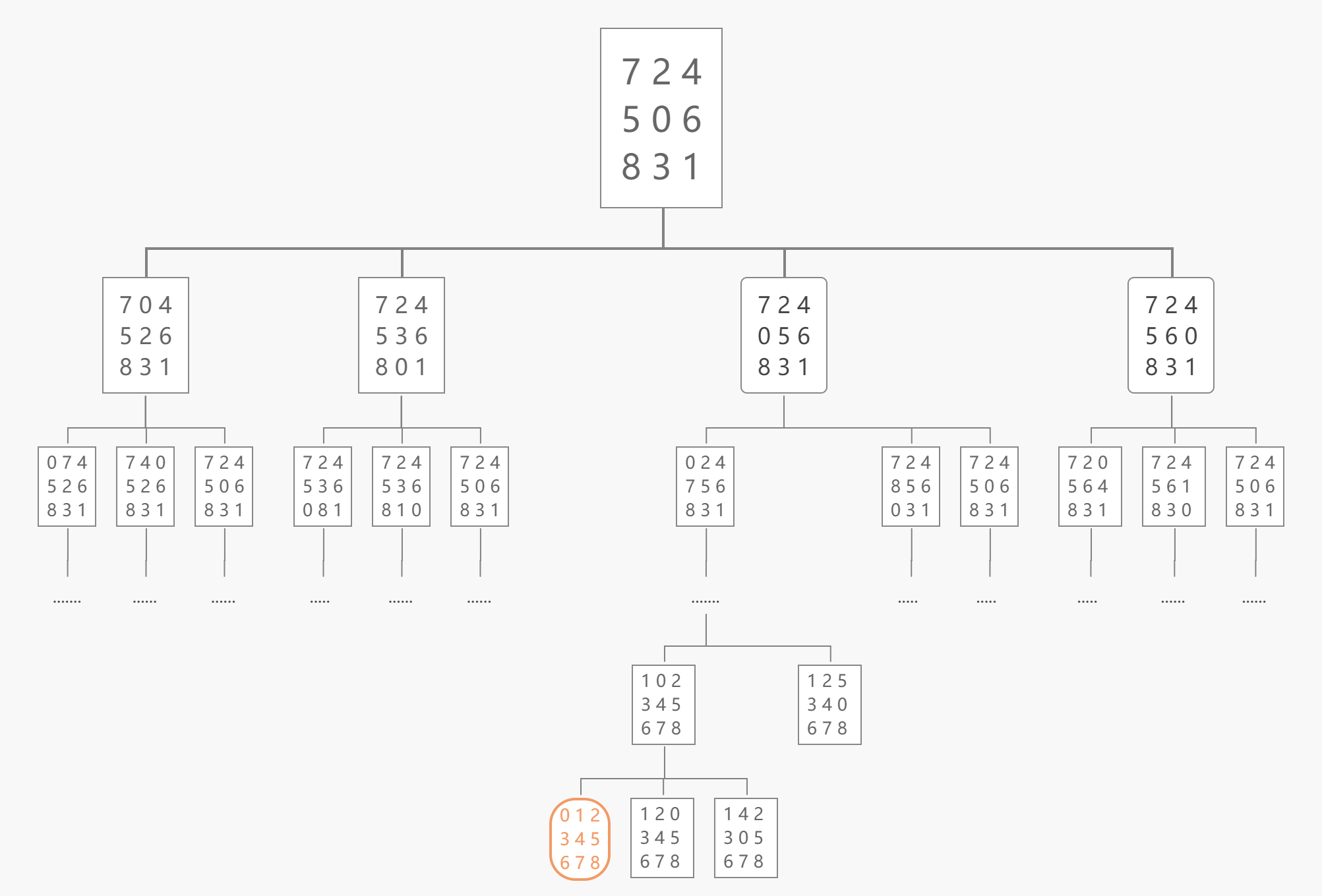
2、图演示:
2.3 路径代价
八数码问题的路径代价可以用由初始状态经过变换成为目标状态所需要的移动步数。也就是完成移动时“空格”的移动次数。
3.搜索算法
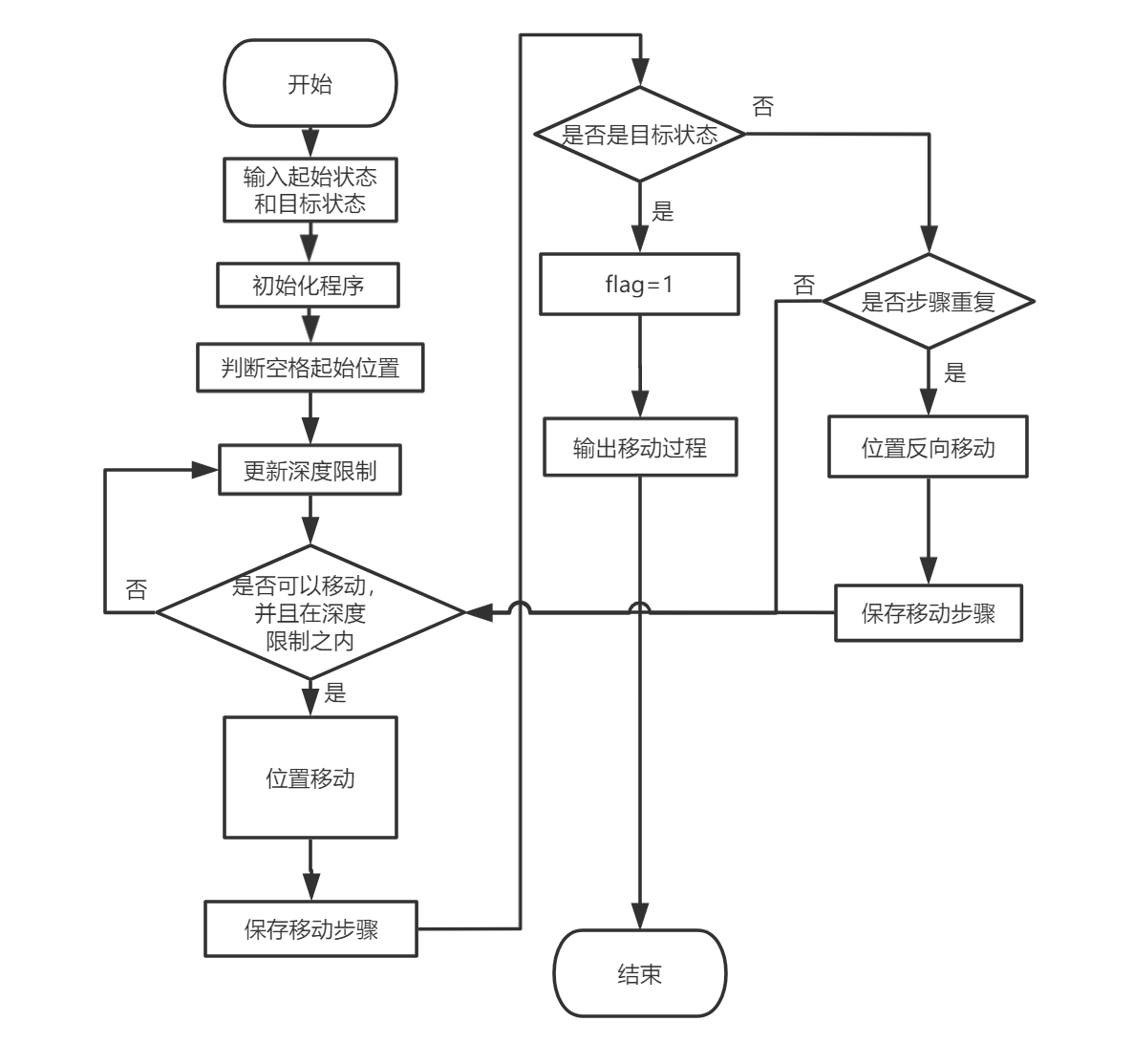
3.1 算法的步骤
1、输入起始状态和目标状态
2、初始化,给定初始数据
3、判断起始状态中空格的位置
4、建立循环,深度限制预设为1
5、进行深度搜索寻找结果
6、更新深度限制,再次进行深度搜索直到成为目标状态
7、结束时输出移动过程
3.2 算法的流程图
4.算法实现
4.1深度限制更新
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
def deepupdate(self):
while(1):
self.numlist=numlist
self.movelist=[]
self.allState=set()
self.solve()
self.deep=self.deep+1
if self.flag==1:
break
print("移动完成_使用迭代加深")
print("零的移动方向:")
self.printRoute()
|
4.2搜索代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
def search(self, direction):
if self.canMove(direction) and len(self.movelist) < self.deep:
self.move(direction)
if self.win == str(self.numlist):
self.flag=1
return True
if str(self.numlist) in self.allState:
self.moveBack(direction)
return False
self.allState.add(str(self.numlist))
searchAll = self.search(2) or self.search(4) or self.search(1) or self.search(3)
if searchAll:
return True
else:
self.moveBack(direction)
return False
else:
return False
|
4.3移动位置代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
def move(self, direction):
if moving.left.value == direction:
self.numlist[self.x][self.y], self.numlist[self.x][self.y - 1] = \
self.numlist[self.x][self.y - 1], self.numlist[self.x][self.y]
self.y = self.y - 1
if moving.right.value == direction:
self.numlist[self.x][self.y], self.numlist[self.x][self.y + 1] = \
self.numlist[self.x][self.y + 1], self.numlist[self.x][self.y]
self.y = self.y + 1
if moving.up.value == direction:
self.numlist[self.x][self.y], self.numlist[self.x - 1][self.y] = \
self.numlist[self.x - 1][self.y], self.numlist[self.x][self.y]
self.x = self.x - 1
if moving.down.value == direction:
self.numlist[self.x][self.y], self.numlist[self.x + 1][self.y] = \
self.numlist[self.x + 1][self.y], self.numlist[self.x][self.y]
self.x = self.x + 1
self.movelist.append(direction)
|
4.4判断是否可以移动
1
2
3
4
5
6
7
8
9
| def canMove(self, direction):
if moving.left.value == direction:
return self.y > 0
if moving.right.value == direction:
return self.y < 2
if moving.up.value == direction:
return self.x > 0
if moving.down.value == direction:
return self.x < 2
|
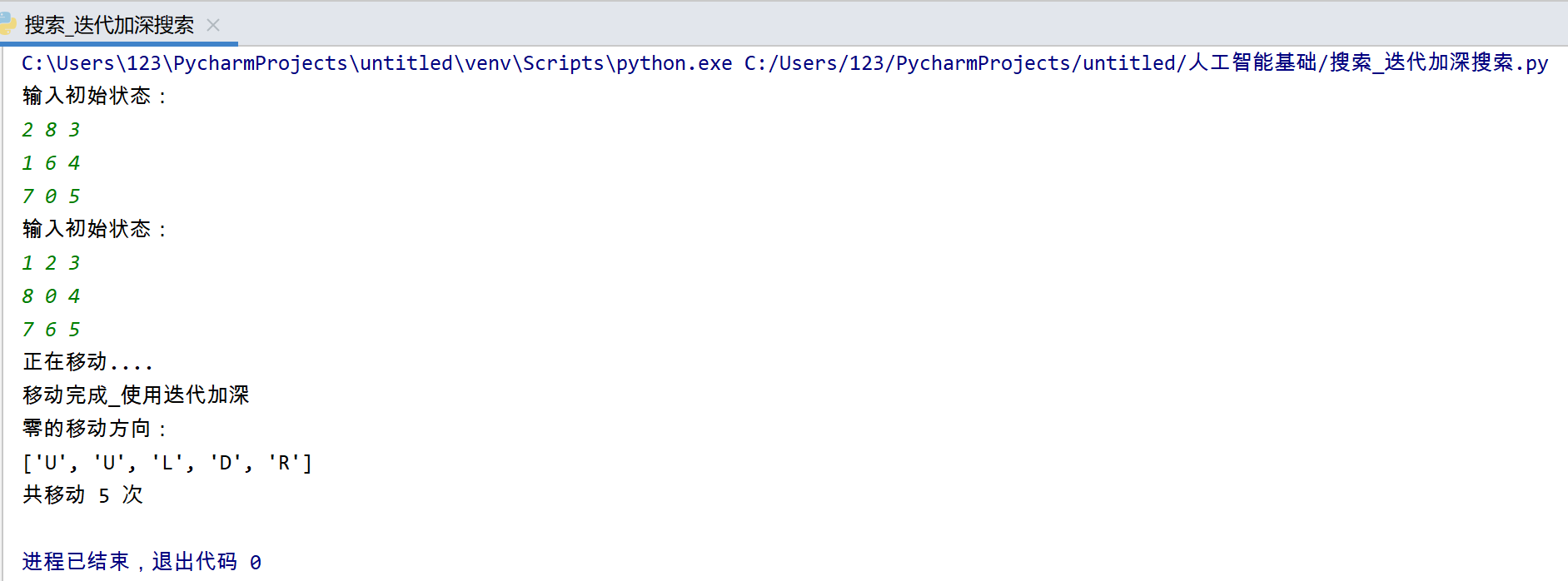
5.结果展示
7 2 4 5 0 6 8 3 1 → 0 1 2 3 4 5 6 7 8
7 2 4 5 0 6 8 3 1 → 1 2 3 4 5 6 7 8 0
2 8 3 1 6 4 7 0 5 → 1 2 3 8 0 4 7 6 5