香农码，费诺码和霍夫曼码的编码方法与简单比较

香农码

编码步骤：

1. 将信源符号的发生概率（降序）排序；
2. 计算各信源符号的自信息量；
3. 码长：自信息量向上取整；（保证是唯一可译码，且无失真编码）
4. 排序后的信源符号，计算累加概率（取左端点）；
5. 累加概率二进制话，取对应码长，得到编码码字；

编码举例：

有a b c d概率分别为：0.25 0.4 0.2 0.15

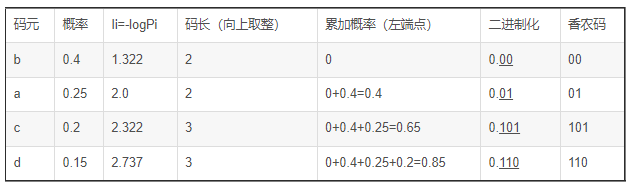
平均码长=(0.4+0.25)*2+(0.2+0.15)*3=2.35

信源熵=0.5328+0.5+0.4644+0.41055=1.90775

编码效率=1.90775/2.35=0.812

---

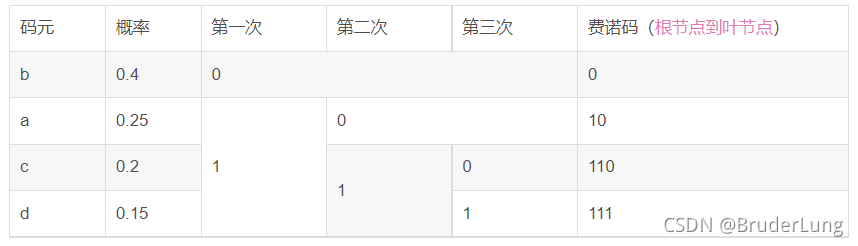
费诺码：

编码步骤：

1. 将信源符号的发生概率排序（为了方便，不是必须的）；
2. 尽可能的等概率划分成两类；
3. 以符号“0”和“1”标识；
4. 直到只有一个符号时结束；

   编码举例：

   

有a b c d概率分别为0.25 0.4 0.2 0.15

平均码长=0.4+0.25*2+(0.2+0.15)*3=1.95

信源熵=0.5328+0.5+0.4644+0.41055=1.90775

编码效率=1.90775/1.95=0.978

---

霍夫曼码：

编码步骤：

1. 按概率递减排序；
2. 将概率最小的两个相加并用“0”和“1”表示，得到新的信源
3. 对新的信源按概率（递减）排序；
4. 重复以上步骤，直到信源只剩两个符号；
5. 然后从叶节点到根节点的顺序，获得编码；

   编码举例：

   过程：

可以得到：

平均码长=0.4+0.25*2+(0.2+0.15)*3=1.95

信源熵=0.5328+0.5+0.4644+0.41055=1.90775

编码效率=1.90775/1.95=0.978

---

比较：

1. 香农编码具有很好的扩展性；
2. 实际的编码效率：霍夫曼>费诺>香农；